Mirrored Delay Line

For an audio processing application I am sampling audio data into a delay line then convolving or cross-correlating in the time domain. For short delay lines it is possible to use the memmove function without having too great an impact on processor time. However, when the delay length increases to several thousand values the processing time required just to append a new sample can have a major impact on the application. I have a requirement to operate in real-time on delay lines of around 8000 values. Looking at the results below we can see how the append operation time varies with delay line length. The Mirrored Delay Line trades processing time for memory, needing double the memory but reducing the append operation time to a constant amount regardless of delay line length.

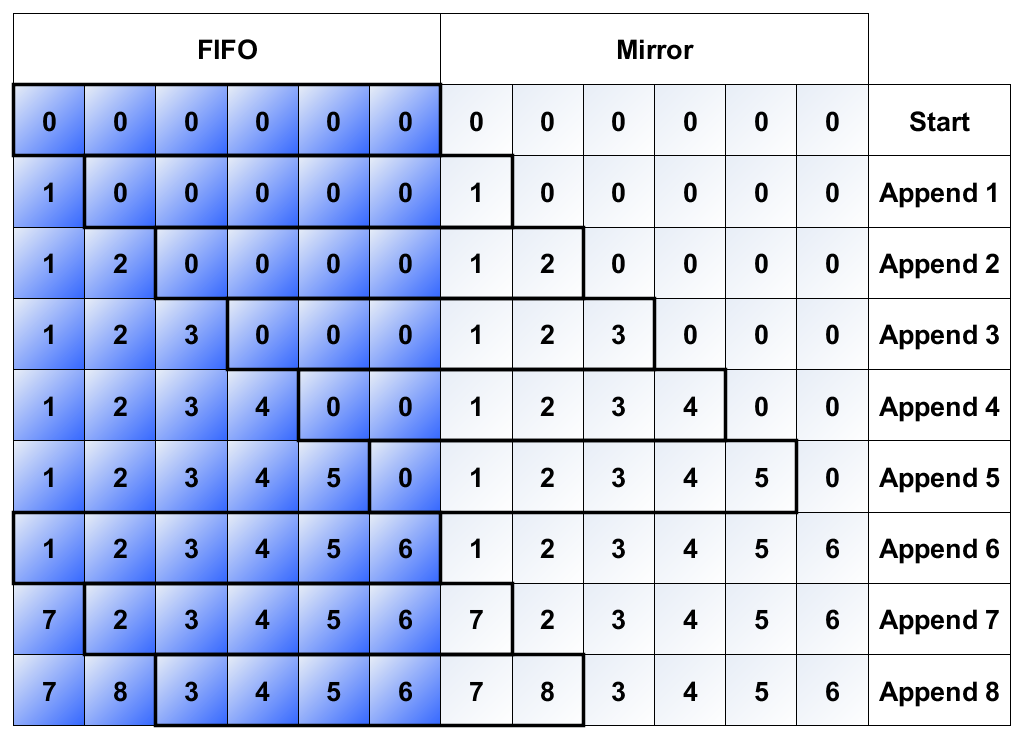
Mirrored delay line

This speeds up the delay line append operation for very long delay lines whilst still allowing access to a single contiguous block of memory for convolution and cross-correlation operations.

Much like the Mirrored FIFO this approach was based on the techniques used in “virtual ring buffers” but without mapping virtual memory. For more information see: The Magic Ring Buffer and Circular (ring) buffer plus neat virtual memory mapping trick posts.

$ ./test.exe
MirroredDelayLine example usage

Initialised delay line:
Contents=[0, 0, 0, 0, 0]
Appending.
0 data()-Contents=[0, 0, 0, 0, 0] [i]-Contents=[0, 0, 0, 0, 0]
1 data()-Contents=[0, 0, 0, 0, 1] [i]-Contents=[0, 0, 0, 0, 1]
2 data()-Contents=[0, 0, 0, 1, 2] [i]-Contents=[0, 0, 0, 1, 2]
3 data()-Contents=[0, 0, 1, 2, 3] [i]-Contents=[0, 0, 1, 2, 3]
4 data()-Contents=[0, 1, 2, 3, 4] [i]-Contents=[0, 1, 2, 3, 4]
5 data()-Contents=[1, 2, 3, 4, 5] [i]-Contents=[1, 2, 3, 4, 5]
6 data()-Contents=[2, 3, 4, 5, 6] [i]-Contents=[2, 3, 4, 5, 6]
7 data()-Contents=[3, 4, 5, 6, 7] [i]-Contents=[3, 4, 5, 6, 7]
8 data()-Contents=[4, 5, 6, 7, 8] [i]-Contents=[4, 5, 6, 7, 8]
9 data()-Contents=[5, 6, 7, 8, 9] [i]-Contents=[5, 6, 7, 8, 9]
Clearing.
Contents=[0, 0, 0, 0, 0]
Timing comparisons.
delayLineLength=100
repetitions=100000000
Starting timing comparison: Naive
Starting timing comparison: Memmove
Starting timing comparison: Mirrored Delay Line
Time per delay line append operation.
Naive = 510.44 ns
Memmove = 28.08 ns
Mirrored Delay Line = 10.76 ns
Timing comparisons.
delayLineLength=2000
repetitions=10000000
Starting timing comparison: Naive
Starting timing comparison: Memmove
Starting timing comparison: Mirrored Delay Line
Time per delay line append operation.
Naive = 10141.6 ns
Memmove = 193.5 ns
Mirrored Delay Line = 10.9 ns
Timing comparisons.
delayLineLength=8000
repetitions=10000000
Starting timing comparison: Naive
Starting timing comparison: Memmove
Starting timing comparison: Mirrored Delay Line
Time per delay line append operation.
Naive = 40613.3 ns
Memmove = 631.8 ns
Mirrored Delay Line = 11 ns

Source code for the library and example is hosted at https://github.com/bensherlock/sherlock-code/blob/master/include/MirroredDelayLine.h .